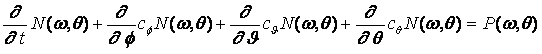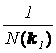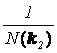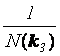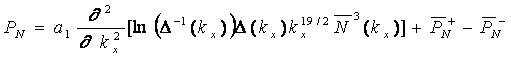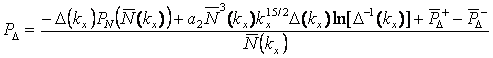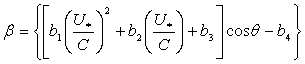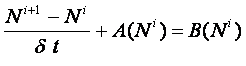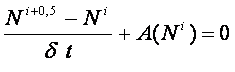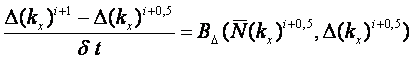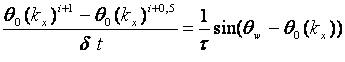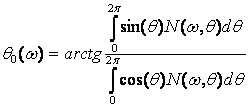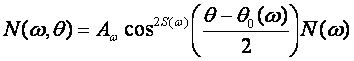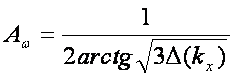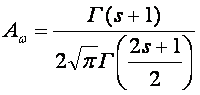Региональный прогноз ветрового волнения в Северной Атлантике

Абузяров Ю.Н (ГМЦ)

Кабатченко И.М. (ГОИН)

Чижиков Д. (МФТИ)

Введение

Под руководством директора Института теоретической физики им. Л.Д. Ландау академика В.Е. Захарова сотрудниками институтов Академии Наук и Росгидромета уже несколько лет разрабатывается модель самосогласованного описания ветра и волн. Эта модель устраняет недостатки самой используемой в настоящее время в мировой науке модели WAM и является, по сути дела, первой в мире моделью следующего (по сравнению с WAM) поколения. Достичь этого качественного улучшения гидродинамических моделей ветровых волн удалось за счет двух основных фундаментальных результатов: построенную В.Е. Захаровым регулярную процедуру упрощения общего интеграла нелинейных взаимодействий и предложенную М.М. Заславским технику самосогласованного описания ветра и волн. Эта техника позволяет описывать совместно два процесса в приповерхностном слое океана – ветровой поток и ветровое волнение. Такой подход дает возможность динамически освещать состояние поверхности океана, в частности эволюцию параметра шероховатости.

Новизна предлагаемых решений заключается в том, что на основе уравнения переноса волнового действия (оно приведено в п. 2.4.1) авторами создана более совершенная гидродинамическая модель эволюции ветрового волнения и разработана численная ее версия. Отличие ее от известных моделей состоит в том, что один из основных членов функции источников и стоков уравнения переноса волновой энергии - член, описывающий нелинейный обмен энергии в спектре волн задан с использованием «узконаправленного» упрощения исходного интеграла. Смысл упрощения заключается в следующем. Интеграл нелинейных взаимодействий (кинетический интеграл) сводится к дифференциальному виду регулярной процедурой разложения исходного интеграла в ряд по "параметру узконаправленности", который оказывается малым для реальных функций углового распределения энергии в двухмерном спектре волн. Предлагаемое упрощение является первой строго обоснованной процедурой среди известных решений. Впервые оно было предложено в работах Захарова В.Е. /1/ и развито Заславским М.М. /2/. Формально оно сходно с известным приближением Хассельмана, использующим для упрощения названного интеграла гипотезу о локальности четырехволновых взаимодействий. Последняя для произвольных спектров ветровых волн, вообще говоря, не выполняется, но как раз в узконаправленном приближении доказывается аналитически. Тем самым можно считать предлагаемый способ рассмотрения интеграла взаимодействий первым и единственным пока с теоретической точки зрения строгим решением.

Всего в мире метеорологическими службами разных стран и частными фирмами применяется несколько десятков (около 50-60) волновых моделей, часть из них – для решения оперативных задач. Если исключить из этого числа устаревшие модели прежних лет, то оставшиеся в концептуальном плане можно разделить на 2 основных больших класса – дискретные и параметрические В свою очередь, они содержат множество модификаций. В первых рассматривается совокупность спектральных составляющих с разными частотами (волновыми числами) и направлениями распространения. В рамках дискретных моделей используется два уровня детализации при описании эволюции волнового поля, характеризуемого спектром:

1)                 Первый уровень основан на численном решении исходного кинетического интеграла. Основной недостаток данного уровня – огромная трудоемкость расчетов, которая исключает применение его при оперативных расчетах и прогнозах волнения. Данный уровень детализации, как правило, используется только при исследовании физики процессов взаимодействия в системе океан-атмосфера;

2)                 Второй уровень – использование аналитических упрощений исходного интеграла. К данному уровню относятся модели WAM /3/ и заявленная модель узконаправленного приближения волнового спектра. Так как в данных моделях исследуется эволюция направленного спектра ветрового волнения для некоторой дискретной области волновых чисел, то данный подход называется спектрально-дискретным. При имеющемся в ГМЦ парке ЭВМ разумнее всего использовать модели данного уровня для регионального моделирования ветрового волнения;

Создание параметрических моделей достигается в рамках третьего уровня детализации – интегрального. Он основан на известном свойстве кинетического интеграла – его консервативности. Интегральный перенос для всех волновых чисел тождественно равен нулю. Задавшись известными теоретическими или эмпирическими спектрами ветрового волнения можно, проинтегрировав кинетическое уравнение, перейти к интегральной его версии. Как правило, при данном уровне детализации исследуется эволюция нескольких интегральных параметров ветрового волнения (как правило, нулевого момента спектра и генерального направления распространения волн). Данный уровень детализации (спектрально-параметрический) разумнее всего использовать в глобальных моделях ветрового волнения из-за относительной простоты исходных уравнений. В настоящее время в оперативной практике ГМЦ используется две такие модели МАК /4/ (принята для оперативного использования в Росгидромете на центральной методической комиссии Гидрометцентра, решение от 22 июля 1990 года) и экспериментальная модель Лавренова /5/. Обе названные модели можно, как видно из определения, отнести к одному классу моделей – параметрическому. В то же время между ними существует заметная разница. В модели МАК уравнение переноса волновой энергии (уравнение (1)) интегрируется по частоте. Полученное в итоге уравнение описывает эволюцию углового спектра общей энергии, что позволяет решить задачу прогноза волн в рамках моделей этого класса более корректно. В модели Лавренова уравнение переноса интегрируется и по направлению. В итоге описывается лишь один параметр волнового спектра – нулевой момент (в прототипной модели JONSWAP только для описания частотного спектра используется 5 параметров, что позволяет достигать более точного описания спектра).

Заявленная модель узконаправленного приближения ветрового волнения является первой спектрально-дискретной моделью, внедряемой для регулярного оперативного применения в ГМЦ РФ. Краткое описание модели и первый опыт ее применения в ГМЦ РФ   в диагностическом и прогностическом режимах будет дан ниже в четырех главах и заключении. В рамках выполнения данного проекта данная модель получила статус Российской Атмосферно-Волновой Модели (решение Научного Технического Совета Росгидромета от 6.7.2001), а метод прогноза ветрового волнения, основанный на применении данной модели был принят в практику оперативных работ Росгидромета (решение Центральной Методической Комиссии Росгидромета от 17.10.2001).

 

 

Краткое описание модели.

Основой модели служит уравнение переноса волнового действия в спектральной форме (Хассельман, /6/):

(1)

где - спектр волнового действия, - частотный спектр, - угловой спектр, f и - сферические координаты-углы, , , , , r - радиус земли, Р - функция источников и стоков, включающая функцию взаимодействия волн и ветра (Р⁺), нелинейные взаимодействия в спектре ветровых волн (Р^±) и диссипацию (Р^-). Наибольшую сложность при решении данного уравнения представляет член нелинейного взаимодействия:

P^±(k)=4pòdk₁òdk₂òdk₃T²(k, k₁, k₂, k₃)N(k)N(k₁)N(k₂)N(k₃)

´[+--] d(w(k) +w(k₁) - w(k₂) -w(k₃))

´d(k + k₁ - k₂ - k₃), (2)

где k – волновое число (для условий глубокого моря, связанное с частотой соотношением w²=gk). Ядро Т данного трехкратного интеграла не приводится из-за его алгебраической громоздкости.

В рассматриваемой модели для описания нелинейных взаимодействий используется теория узконаправленного приближения волнового спектра. В рамках этой теории от двухмерного спектра N(w,q) переходят к двум интегральным функциям – спектру волновых чисел `N(k_x) и параметру узконаправленности D(k_x).

(3)

(4)

(5)

где k_y - координата в пространстве волновых чисел перпендикулярная k_x, а направление k_x совпадает с направлением ветра. В этом случае функция источников и стоков может быть записана следующим образом

_, (6)

_, (7)

где P_N и P_D - функции источников и стоков для N(k_x) и D(k_x) соответственно, , , , .

Функция взаимодействия волн и ветра

Р ⁺=b N(w,q), (8)

где для задания коэффициента b используется эмпирическая аппроксимация /7/:

, (9)

U_**- динамическая скорость ветра, С – фазовая скорость волн, b₁ = 4*10^-2; b₂ = 5,44*10^-3; b₃ = 5,5*10^-5; b₄ = 3,1*10^-4.

Для описания диссипации используется представление о блокировочном интервале спектра. Считается что рост спектральной плотности волнового действия невозможен выше блокировочного спектра

. (10)

Если вычисленный спектр превышает величину , то разность между ним и блокировочным спектром и представляет собой функцию `Р^- .

Численно уравнение (1) решается методом расщепления по физическим процессам /8/. При этом левая часть уравнения учитывалась для двухмерного спектра волнового действия, а правая для двух интегральных функций

(11)

где - значения N(w,q) на последующем и предыдущем шаге модели, A(N) - адвективный член, В(N) - функция источников и стоков (численный аналог функции Р). На первом полушаге

. (12)

На втором полушаге

. (13)

Далее (13) можно переписать в виде двух уравнений для частотного спектра волнового действия и параметра узконаправленности:

(14)

и

. (15)

Для численного расчета функции источников и стоков использовался программный продукт «Думка» /9/.

Узконаправленная теория ветрового волнения разработана для случая, когда преобладающее направление распространения волнения (q₀) совпадает с направлением ветра и угловой спектр имеет симметричную форму. В реальных нестационарных и неоднородных полях ветра наблюдается рассогласование направлений ветра и генерального направления волн. Так как теория не описывает процесс подстройки генерального направления распространения волн к направлению ветра, в настоящей модели использована эмпирическая формула, описывающая этот процесс. Она имеет вид /10/:

, (16)

где - время подстройки, эмпирическая константа b=10^-4. Для определения q₀ по двухмерному спектру ветровых волн применяется соотношение

Обратное преобразование из интегральных функций в двухмерный спектр осуществляется следующим образом:

. (17)

Нормирующий множитель при косинусоидальной аппроксимации углового спектра A_w функционально связан с параметром узконаправленности и степенью при косинусе:

, (18)

_., Г - гамма-функция

Специальные исследования буйковых и других измерений спектра N(w,q) показало, что гипотеза узконаправленности строго выполняется в основном энергонесущем его диапазоне. При современном уровне развития волноизмерительной техники проверку параметра D(w) на основе измерений можно осуществить с намного большей достоверностью, чем функции j(w,q). Оказывается, что справедливость формы этой последней невозможно ни подтвердить, ни опровергнуть на основе современных измерений. Поэтому можно утверждать, что модель узконаправленного приближения представляет собой оптимальное решение задач расчета и прогноза волн при современном уровне развития вычислительной и измерительной техники.

Конфигурация модели.

При расчете полей волнения в Северной Атлантике использовалось разрешение 2,5⁰ широты на 2,5⁰ долготы. Для расчета волнения в диагностическом режиме использовались поля давления объективного анализа Багрова (далее эти поля по специальной процедуре пересчитывались в поля динамической скорости ветра). Считается, что для формирования поля волнения в Северной Атлантики достаточно 1,5 – 2 суток. Поэтому при расчетах использовались поля давления на срок расчета и предшествующие ему на 36, 24, 12 часов. На границе сеточной области задавались климатические спектры ветрового волнения. Существующая глобальная спектрально-параметрическая модель волнения рассчитывает лишь интегральные характеристики волнения, которые неприменимы в дискретных моделях. Расчет велся по 2 синоптическим срокам (0, 12 час. времени Гринвического меридиана). Для прогноза волнения использовались поля приземного атмосферного давления расчитанные по модели СМ-15. Предельная заблаговременность 72 ч. На выходе модели выдаются прогнозы волнения на 12, 24, 36, 58, 60 и 72 часа.

 

 

 

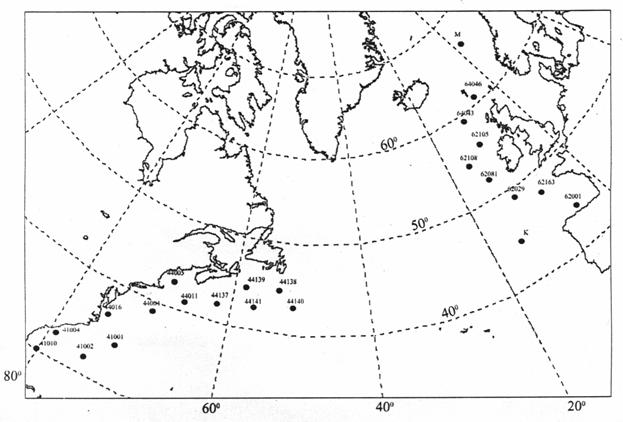
Верификация модели по натурным данным в диагностическом режиме

В Северной Атлантике, расположено всего порядка 40 английских, американских и канадских волноизмерительных буев и три «корабля погоды» (рис. 1), на которых также измеряются параметры волнения. Альтернативными им являются визуальные наблюдения с попутных кораблей и измерения со спутников. Оба эти источника волновой информации обладают специфическими недостатками. Визуальные наблюдения сильно разняться по точности, потому что существенно зависят от подготовленности штурманов, которые, как правило, и ведут эти наблюдения. Спутниковые измерения характеризуются относительно большим временем опроса (периодом, через который они пролетают над конкретной точкой Земной поверхности) - от 20 до 40 суток. В целом, обладая достаточной точностью, эти измерения не могут быть использованы для изучения такого важного масштаба изменчивости, как синоптический (характерные периоды синоптической изменчивости меньше периода опроса спутников). Все вышесказанное приводит к тому, что верификацию моделей волнения разумнее всего проводить при помощи волновых буев и кораблей погоды.

Модель верифицировалась в диагностическом режиме. За конкретный срок результаты наблюдений с буев и кораблей погоды усреднялись для Северной Атлантики (`h<sub>ф</sub>), также усреднялись и все рассчитанные высоты волн (`h_р). Сравнение (табл. 1) велось для этих осредненных величин. В таблице приведен скаттер-индекс* SI (%), который характеризует степень расхождение между рассчитываемыми и наблюдаемыми значениями высоты волны в конкретных точках. Чем он меньше, тем расчеты достовернее. В целом следует признать результаты сравнения исключительно удачными. Во всех случаях индекс SI не превысил 30% (уровень, меньше которого расчеты считаются удовлетворительными, составляет 40%). Обращает на себя внимание, что в расчетах имелась систематическая ошибка, занижающая волны. Анализ ее привел к выводу о том, что при расчетах была принятая необоснованная гипотеза о нейтральной стратификации приводного слоя атмосферы.

Рис. 1 Расположение океанских буев в Северной Атлантике.

 

После введение в модель условия слабой неустойчивости атмосферы, волны подрастут, и это повысит точность расчетов.

*) Примечание: Формула для SI сходна с известным коэффициентом вариации. В отличие от него нормировка среднеквадратичной разности между измеренным и рассчитанным значениями изучаемого параметра (в данном случае, высоты волн) осуществляется на «текущее» среднее его значение, а не генеральное среднее. Такой подход позволяет более корректно описывать быстро меняющиеся во времени процессы.

 

Таблица 1.

Результаты оценок диагностических расчетов высот волн по узконаправленной модели ветрового волнения и данным стационарных буев в Северной Атлантике

 

Верификация модели по натурным данным в прогностическом режиме

В начале 2002 года модель узконаправленного приближения ветрового волнения была внедрена в практику оперативных прогнозов ВЦ ГМЦ. Сведения о записях результатов расчета по данной модели в базе данных прогноз приведены в таб. 2. Предварительно модель была протестирована в прогностическом режиме. Для сравнения с данными расчетов по модели использовались данные буйковых наблюдений в Северной Атлантике (рис.1). span>Оценка качества модели производилась в соответствии с нормативным документом /11/. Результаты тестирования приведены в таб. 3 и 4. Они свидетельствуют о высоком качестве модели. Также обращает на себя внимание то, что качество прогнозов не сильно зависит от заблаговременности.

 

Таблица 2.

СВЕДЕНИЯ О ЗАПИСЯХ

размещаемых в базах данных банка данных ПРОГНОЗ на ЭВМ CRAY Y-MP8E

Пользователь Кабатченко Код программы 600405 Имя базы данных SHOT

 

 

Но- мер за- пи- си	Вид обра- ботанных данных: анализ, прогноз, среднее, изменение, климат, таблицы, макеты и др.	Хранимая   величина	Поверх- ность или уровень	Срок наблю- дений (00, 06, 12, 18) или стати- ческая часть	За- бла- го- вре- мен- ность (в часах)	Еди- ница из- ме- ре ния	Точ- ность (коли- чес- тво зна- ков после запя- той)	Тип данных: действи- тельный, целый, код-1 , код-2, код -4, код-8	Размер записи		Диапазон изменения хранимой величины		Имя записи (заполняется администратором баз данных)
									по стро- кам	по столб- цам	минима- льное значение	максима- льное значение
1	2	3	4	5	6	7	8	9	10	11	12	13	14
	прогноз	высота волн	уровень	0	с 12-72 ч.	м	1	действ.	25	45	0	99	J98R***A
	прогноз	направление волн	уровень	0	с 12-72	град.	0	действ.	25	45	0	360	X98R***A

 

Таблица 3.

Обобщенные результаты оценок прогнозов высот волн в Северной Атлантике

 

Таблица 4.

Таблица оправдываемости прогнозов высот волн различной заблаговременности в Северной Атлантике

 

№ п/п	Дата	Исход, срок (ч.)	12 ч.		24 ч.		36 ч.		48 ч.		60 ч.		72 ч.
			N	Q	N	Q	N	Q	N	Q	N	Q	N	Q
1	30.12.99	12	10	90	10	70	13	85	10	60	8	82	13	69
2	18.01.00	12	13	85	19	76	12	83	И	55	10	70	15	73
3	26.01.00	12	22	77	21	77	21	81	21	71	19	50	20	55
4	27.01.00	12	12	75	16	81	9	67	16	56	17	76	17	76
5	31.01.00	12	14	74	19	77	14	79	13	69	18	67	12	67
6	03.02.00	12	21	73	20	76	22	83	20	80	20	80	20	70
7	14.02.00	12	21	86	22	77	22	73	22	59	22	86	21	76
8	23.03.00	12	12	75	18	73	10	70	12	75	12	67	13	75
9	19.04.00	12	17	88	17	82	13	82	13	77	17	76	17	71
10	21.04.00	12	18	67	17	94	18	83	18	89	17	76	18	78
11	24.04.00	12	21	81	12	92	17	47	15	73	15	53	17	72
12	26.04.00	12	16	67	18	84	14	86	14	79	15	87	15	67
13	27.04.00	12	17	82	18	74	17	74	18	78	14	64	17	54
14	28.04.00	12	15	98	16	75	14	86	17	82	16	74	16	60
15	Среднее		245	80	259	79	231	77	237	72	237	72	246	70

 

Условные обозначения: N – число использованных буйковых измерений, Q – процент оправдавшихся прогнозов.

 

 

Литература

1.Захаров В.Е., Смилга А. О квазиоднородных спектрах слабой турбулентности.- Журн. эксп. и теор. физ., 1981, т.81, вып.4(10), с.318-326.

2. Заславский М.М. Об узконаправленном приближении кинетического уравнения для спектра ветровых волн. - Изв. АН СССР. Физика атмосферы и океана. 1989 т.25, N4.

3. The WAM model – a third generation ocean ocean prediction model. - J. Phys. Ocean.1988. v.12. p. 1775 – 1810

4. Абузяров З.К., Матушевский Г.В., Кабатченко И.М. Прогноз волнения в океане на основе параметрической интегральной модели. – Труды ГМЦ, вып. 314, 1991 г. с.60-68

5. Лавренов И.В. Математическое моделирование ветрового волнения в пространственно неоднородном океане. – СПб, Гидрометеоиздат, 1998.

6. Hasselmann K. On the nonlinear energy transfer in a gravity wave spectrum.Pt.1 - J. Fluid Mech., 1962, v.12, p.481-500.

7. Yan. L. An improved wind input source term for third gen­eration ocean wave modelling. - Rep. No. 87-8. 1987: Royal Dutch Meteor. Inst. 20pp.

8. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики - «Наука», Новосибирск, 1967, стр. 196

9. Lebedev V.I. An introduction to functional analysis and computational mathematics. - Birkhauser. 1997.

10. Hasselman K., Dunkel M., Ewing J. Directional wave spectra observed during JONSWAP (1973) -J. Phys. Ocean.1980. v.10. 1980, p. 1264 - 1280.

11. Наставление службе по морским гидрологическим прогнозам. Вып. 9, часть 3, ГИМИЗ. Л., 1982.